(Not actually the Racks and Tubes)
Racks and Tubes are one of those iconic Montessori materials (well, at least to those of us in the field), and it's hard to imagine running a classroom without them. But I have to confess, I have a love-hate relationship with the material. Some of that is simply practical: it's a complicated material with a lot of moving parts, the lesson requires a careful choreography on the part of the guide, and some days we spend more time picking up beads that have been knocked onto the floor than actually doing math. It's also a beautiful material that facilitates not only development of long division, but teamwork, communication, and patience.
The bigger issue to me though, is that it doesn't always work as a pedagogical tool. There are many stages to the Racks and Tubes, and children usually work with them over three or four years. In theory, the material facilitates an understanding of the relationship between the decimal system and long division, but in my experience, some children can repeat the process over and over, solving dozens of division problems, and never figure out what it is they are actually doing. Even the ones who appear successful--that is, they learn the long division algorithm--don't necessarily go into middle school with a clear idea of what division does. (See note below on this latter part.)
I've come to the conclusion that this is because such a complex material needs a narrative to go with it. We humans are meant to think in situations and stories. Abstractions are great once we understand something so well that we don't need to think about it anymore, but not so great for learning. This is the story I invented for some of the learning support students I work with. It's silly, but it's been hugely successful. On the theory that many heads are better than one, I offer it here for you to use and improve on. I'd be grateful if you share your experiences and improvements.
The Story
Let's imagine that we've finally found a reasonable candidate vaccine for COVID-19, and we are getting ready to run a clinical trial. (Actually, I usually do this story with candy. The children get to pick what kind of candy they want to use in the problem, so long as it's not skittles.) We have 7,565 doses to use in the trial, which we are going to share equally between five clinics in five different cities. The clinics want to know how many participants they need to get signed up for the trial and we want to know how many doses to send to each clinic.
Now, we don't really want piles of vaccine doses floating around, so we've packaged them in bags of ten doses. That still leaves us with lots of little bags of vaccine doses floating around, so we've packaged the bags into boxes that each contain ten bags. (Depending on how well I think the children understand the decimal system and how confident they are, I'd probably stop at this point and ask them how many doses are in each box, or just tell them that there are 100 doses in each box.)
In order to avoid having all these boxes stacked up around our lab, we've put them into crates that hold ten boxes each. Of course, our doses don't add up to a perfect multiple of 1,000, so we still have some spares.
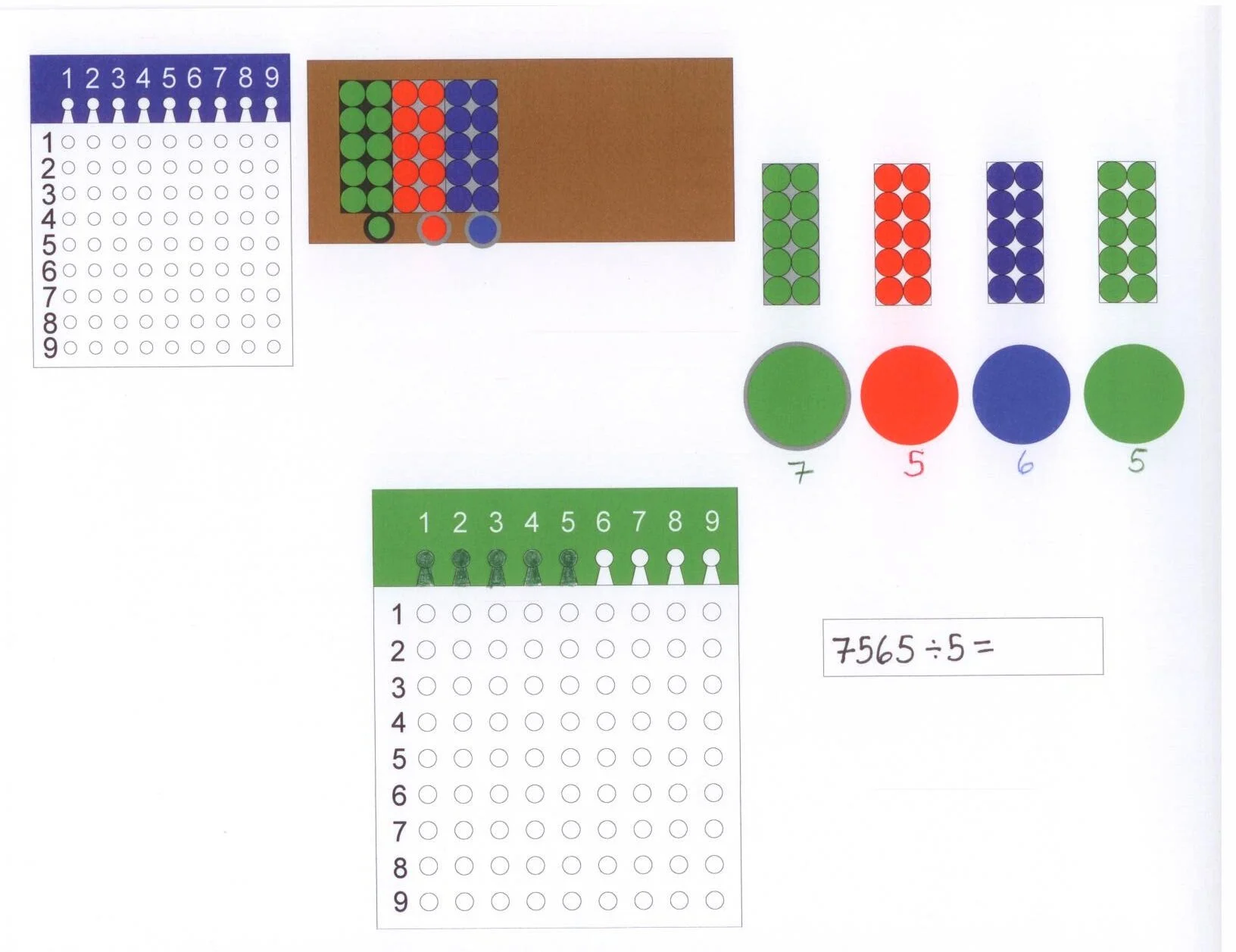
At this point, we start setting up the Racks and Tubes, noticing that in the thousands cup, we have 7 beads, which stands for the seven full crates. But we have one crate that's only partly full, containing those extra 565 doses. So we represent those with the other cups. The 5 boxes of a hundred doses goes in the hundreds cup, the 6 bags of ten doses goes in the tens cup, and the 5 loose doses go in the units cup. (This is an excellent time to laugh about how ridiculous the scientists' packing job is. In my experience, as long as we don't pretend that a ridiculous scenario makes sense, the children will run with it.)
Now that we've set up our cups to represent the doses of the vaccine, let's put five skittles on the board to represent the five different clinics.
The Racks and Tubes set up for our problem
Now I ask the children whether it makes more sense to start with the whole crates or with the remaining individual doses, or somewhere in the middle. To most children, it seems obvious that they should share out the whole crates first, and then deal with the leftovers, but not always. In truth, you can start the sharing out anywhere. You'll get the correct answer, but you'll have to do a lot more repetition and adjusting of digits in your quotient. The more I've thought about this, the more I think I'd prefer to let children discover this for themselves if they choose not to start with the largest category, rather than directing them to do it the “standard” way.
But let's assume we decide to start with the full crates. Then we can share a thousand bead (representing the crates) to each clinic:
Racks and Tubes after sharing out the thousands
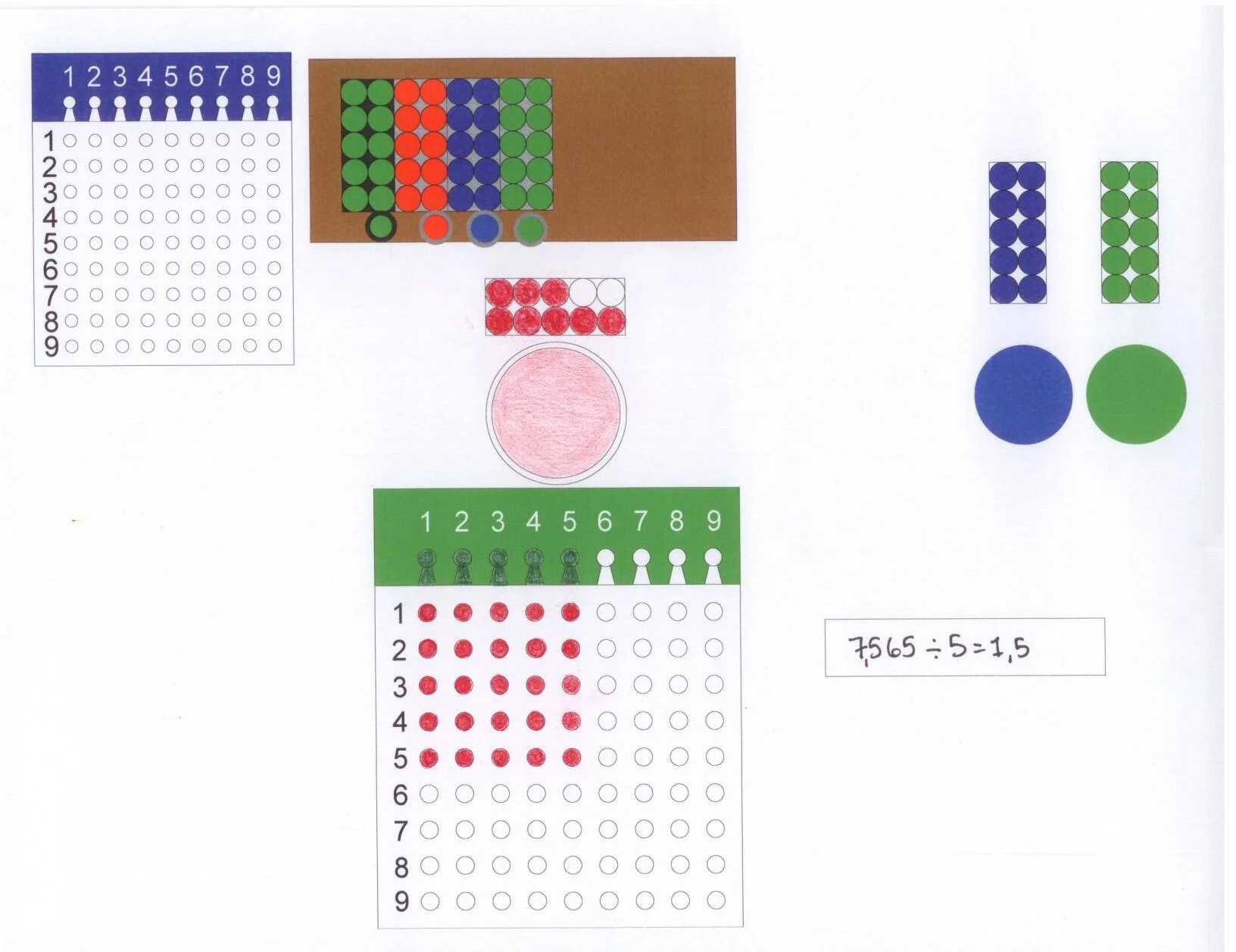
So now each clinic is going to get one full crate of 1000 doses of the vaccine, but we have two extra crates left over. There obviously aren't enough to give every clinic a full crate, so our best bet is going to be to open up the crates and pull out the boxes inside. When we pull out the ten boxes from inside each crate and add them to the five loose boxes we already had, we have 25 boxes of 100 doses each, we'll represent that by exchanging each of the remaining thousand beads for ten hundred beads. Now we can figure out how many boxes each clinic should get:
Racks and Tubes after sharing out the hundreds
By now, the pattern should be clear. We were able to share out all the boxes, so we just need to deal with those six bags of ten doses, plus the remaining five loose doses. We'll do that the same way: each clinic will get one bag of ten doses, and then we'll have to open that last back, pull out the individual doses, and add them to the five loose doses we already have--15 doses. We share those out, record the totals, and we're done:
By the way, this strategy works at any stage of learning the Racks and Tubes. You can do it with the simplest possible recording, simply writing down each digit of the answer, or with full long division. It doesn't matter.
Parent Coaching
Are you trying to help your child learn division? I can help! I now offer coaching for parents. During these Zoom sessions, we will explore your particular situation exclusively, and come up with a plan for your next steps. Sign up today!
photo credit: valilouve <a href="http://www.flickr.com/photos/8471692@N07/533075765">Calcul</a> via <a href="http://photopin.com">photopin</a> <a href="https://creativecommons.org/licenses/by-nc-sa/2.0/">(license)</a>